HIMPUNAN
MATA KULIAH :
MATEMATIKA DAN ILMU ALAMIAH DASAR
NAMA PENGAJAR :
ISHAQ
NAMA PENGAJAR :
ISHAQ
Disusun Oleh:
KELOMPOK 1 – 1PA08
1. Agustin Tiara Yuti (10515313)
2. Nadaa Savira Syahlaa (14515902)
3. Ni Made Puspa A. (15515031)
4. Oktaviani Widhi A. (15515266)
5. Putra Dirgantara (15515421)
6. Ridha Khansa D.K (15515920)
FAKULTAS PSIKOLOGI
UNIVERSITAS
GUNADARMA
TAHUN AJARAN 2015-2016
Himpunan
Dalam matematika, himpunan adalah segala koleksi benda-benda tertentu yang dianggap sebagai satu kesatuan. Walaupun hal ini merupakan ide yang sederhana, tidak salah jika himpunan merupakan salah satu konsep penting dan mendasar dalam matematika modern, dan karenanya, studi mengenai struktur kemungkinan himpunan dan teori himpunan, sangatlah berguna.
Himpunan dalam matematika diartikan sebagai kumpulan dari objek yang terdefinisikan dengan jelas. Himpunan memiliki anggota yang tunggal dimana tidak ada anggota yang sama dalam satu himpunan. Kumpulan dari semua anggota yang terdapat dalam sebuah himpunan dinamakan dengan himpunan semesta (S).
Ø Notasi Himpunan
Biasanya, nama himpunan ditulis menggunakan huruf besar, misalnya S, A, atau B, sementara anggota himpunan ditulis menggunakan huruf kecil (a, c, z). Cara penulisan ini adalah yang umum dipakai, tetapi tidak membatasi bahwa setiap himpunan harus ditulis dengan cara seperti itu. Tabel di bawah ini menunjukkan format penulisan himpunan yang umum dipakai.
| Nama | Notasi | Contoh |
|---|---|---|
| Himpunan | Huruf besar |  |
| Anggota himpunan | Huruf kecil (jika merupakan huruf) |  |
| Kelas | Huruf tulisan tangan | 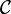 |
Himpunan-himpunan bilangan yang cukup dikenal, seperti bilangan kompleks, riil, bulat, dan sebagainya, menggunakan notasi yang khusus.
| Bilangan | Asli | Bulat | Rasional | Riil | Kompleks |
|---|---|---|---|---|---|
Notasi
|  |  |  |  |  |
Ø Simbol-simbol khusus yang dipakai dalam teori himpunan
Simbol-simbol khusus yang dipakai dalam teori himpunan adalah:
Simbol
|
Arti
|
|---|---|
 atau atau  | Himpunan kosong |
 | Operasi gabungan dua himpunan |
 | Operasi irisan dua himpunan |
 , ,  , ,  , ,  | Subhimpunan, Subhimpunan sejati, Superhimpunan, Superhimpunan sejati |
 | Komplemen |
 | Himpunan kuasa |
Ø Operasi Himpunan
v Gabungan
Dua himpunan atau lebih yang digabungkan bersama-sama. Operasi gabungan = A ∪ B setara dengan A or B, dan anggota himpunannya adalah semua anggota yang termasuk himpunan A ataupun B. A ᴜ B = {x | x ϵ A atau x ϵ B}
Contoh:
A = {2,3,4,5}
B = {4,5,6,7}
AᴜB = {2,3,4,5,6,7}
Beberapa sifat dasar gabungan:
§ A ∪ B = B ∪ A.
§ A ∪ (B ∪ C) = (A ∪ B) ∪ C.
§ A ⊆ (A ∪ B).
§ A ∪ A = A.
§ A ∪ ∅ = A.
§ A ⊆ B jika and hanya jika A ∪ B = B.
v Irisan
Operasi irisan A ∩ B setara dengan A dan B. Irisan merupakan himpunan baru yang anggotanya terdiri dari anggota yang dimiliki bersama antara dua atau lebih himpunan yang terhubung. Jika A ∩ B = ∅, maka A dan B dapat dikatakan disjoint (terpisah).
Contoh:
A = {2,3,4,5}
B = {4,5,6,7}
A∩B = {4,5}
Beberapa sifat dasar irisan:
§ A ∩ B = B ∩ A.
§ A ∩ (B ∩ C) = (A ∩ B) ∩ C.
§ A ∩ B ⊆ A.
§ A ∩ A = A.
§ A ∩ ∅ = ∅.
§ A ⊂ B jika and hanya jika A ∩ B = A.
v Selisih
Selisih adalah himpunan yang anggotanya semua anggota A tetapi bukan anggota dari B. A-B = {x|x ϵ A atau x Ϊ B}
Contoh:
A = {1,2,3,4,5,}
B = {2,3,5,7,11}
A-B = {1,4}
v Komplemen
Komplemen adalah suatu himpunan yang anggota-anggotanya merupakan anggota S tetapi bukan anggota A.
Komplemen A ditulis A1 atau Aᶜ = {x|x ϵ S dan x Ϊ A}
Contoh:
A = {1,2,…,5}
B = {bil. Asli kurang dari 10}
Aᶜ = {6,7,8,9}
Ekstensi dari komplemen adalah diferensi simetris (pengurangan himpunan), jika diterapkan untuk himpunan A dan B atau A - B menghasilkan
Contohnya, diferensi simetris antara:
· {7,8,9,10} dan {9,10,11,12} adalah {7,8,11,12}.
· {Ana,Budi,Dedi,Felix} dan {Cici,Budi,Dedi,Ela} adalah {Ana,Cici,Ela,Felix}.
Untuk menyatakan sebuah himpunan ada 4 cara, yaitu:
• Enumerasi
Enumerasi yaitu mendaftarkan semua anggota himpunan. Jika terlampau banyak tetapi mengikuti pola tertentu, dapat digunakan elipsis (...).
contoh: x = {s,a,p,i}
• Simbol Baku
Simbol Baku ada beberapa simbol tertentu yang sudah disepakati untuk menyatakan sebuah himpunan. Misalnya simbol P yang biasa digunakan untuk himpunan bilangan bulat positif, dan huruf R digunakan untuk menyatakan sebuah himpunan yang berisi bilangan riil.
• Notasi Pembentukan Himpunan
Notasi Pembentukan Himpunan adalah himpunan juga bisa dinyatakan dengan cara menulis ciri-ciri umum dari anggota yang ada di dalam himpunan tersebut.
contoh: A = {x|x adalah himpunan bil. Riil}
• Diagram Venn
Diagram Venn adalah cara menyatakan sebuah himpunan dengan menggaambarkannya dalam bentuk grafis.
Ø Relasi antar himpunan
· Himpunan bagian
Dari suatu himpunan, misalnya A = {apel, jeruk, mangga, pisang}, dapat dibuat himpunan-himpunan lain yang anggotanya adalah diambil dari himpunan tersebut.
§ {apel, jeruk}
§ {jeruk, pisang}
§ {apel, mangga, pisang}
Ketiga himpunan di atas memiliki sifat umum, yaitu setiap anggota himpunan itu adalah juga anggota himpunan A. Himpunan-himpunan ini disebut sebagai himpunan bagian dari A. Jadi dapat dirumuskan:
B adalah himpunan bagian dari A jika setiap anggota B juga terdapat dalam A.
Kalimat di atas tetap benar untuk B himpunan kosong. Maka juga subhimpunan dari A.
Untuk sembarang himpunan A,
Definisi di atas juga mencakup kemungkinan bahwa himpunan bagian dari A adalah A sendiri.
Untuk sembarang himpunan A,
Istilah subhimpunan dari A biasanya berarti mencakup A sebagai himpunan bagiannya sendiri. Kadang-kadang istilah ini juga dipakai untuk menyebut himpunan bagian dari A, tetapi bukan A sendiri. Pengertian mana yang digunakan biasanya jelas dari konteksnya.
· Himpunan bagian sejati dari A menunjuk pada himpunan bagian dari A, tetapi tidak mencakup A sendiri.
· Superhimpunan
Kebalikan dari subhimpunan adalah superhimpunan, yaitu himpunan yang lebih besar yang mencakup himpunan tersebut.
· Kesamaan dua himpunan
Himpunan A dan B disebut sama, jika setiap anggota A adalah anggota B, dan sebaliknya, setiap anggota B adalah anggota A.
Definisi di atas sangat berguna untuk membuktikan bahwa dua himpunan A dan B adalah sama. Pertama, buktikan dahulu A adalah subhimpunan B, kemudian buktikan bahwa B adalah subhimpunan A.
· Himpunan Kuasa
Himpunan kuasa atau himpunan pangkat (power set) dari A adalah himpunan yang terdiri dari seluruh himpunan bagian dari A. Notasinya adalah .
Jika A = {apel, jeruk, mangga, pisang}, maka :
{ { },
{apel}, {jeruk}, {mangga}, {pisang},
{apel, jeruk}, {apel, mangga}, {apel, pisang},
{jeruk, mangga}, {jeruk, pisang}, {mangga, pisang},
{apel, jeruk, mangga}, {apel, jeruk, pisang}, {apel, mangga, pisang}, {jeruk, mangga, pisang},
{apel, jeruk, mangga, pisang} }
Banyaknya anggota yang terkandung dalam himpunan kuasa dari A adalah 2 pangkat banyaknya anggota A.
Ø Kelas
Suatu himpunan disebut sebagai kelas, atau keluarga himpunan jika himpunan tersebut terdiri dari himpunan-himpunan. Himpunan A = {{a, b}, {c, d, e, f} , {a, c}, {,} }adalah sebuah keluarga himpunan. Perhatikan bahwa untuk sembarang himpunan A, maka himpunan kuasanya, , P (A) adalah sebuah keluarga himpunan.
Contoh berikut, P = {{a, b}, c} bukanlah sebuah kelas, karena mengandung anggota c yang bukan himpunan.
Ø Kardinalitas
Kardinalitas dari sebuah himpunan dapat dimengerti sebagai ukuran banyaknya anggota yang dikandung oleh himpunan tersebut. Banyaknya anggota himpunan {apel, jeruk, mangga, pisang} adalah 4. Himpunan {p ,q, r, s} juga memiliki anggota sejumlah 4. Berarti kedua himpunan tersebut ekivalen satu sama lain, atau dikatakan memiliki kardinalitas yang sama.
Dua buah himpunan A dan B memiliki kardinalitas yang sama, jika terdapat fungsi korespondensi satu-satu yang memetakan A pada B. Karena dengan mudah kita membuat {(apel, p), (jeruk, q), (mangga, r), (pisang, s)} fungsi yang memetakan satu-satu dan kepada himpunan A ke B, maka kedua himpunan tersebut memiliki kardinalitas yang sama.
Soal-soal :








Tidak ada komentar:
Posting Komentar